Revision as of 16:24, 22 May 2013

Quick Overview

For quick start, please note 3 inputs. We we will name them: 1st, 2nd and 3rd — from left to right. Please also note 2 buttons: Run and Load.

1st input - init state

You enter the init state of qubits here. A decimal integer is required here. Its binary representation defines the start states of the qubits in qregister. Qubit 0 is at the top.

2nd input - qubit signature

You enter a list of integers here in the following format: [qubit1, qubit2, ..., qubitn]. This qubit signature is used for displaying probabilities.

Suppose you have entered [3,4] and that the list of probabilities is:

01 : 0.3 (1)
10 : 0.7 (2)

It simply means that a lot of hypothetical measurements would show that Prob(qubit 4 is in state 0 AND qubit 3 is in state 1) = 0.3 and Prob(qubit 4 is in state 1 AND qubit 3 is in state 0) = 0.7.

Formally, the result is a list of integers with a given probability. The n-th bit of the chosen integer (from the right) represents the state of the qubit which is listed as n-th in the qubit signature (from the left) after the hypothetical measurement. Note these integers are given in binary and in decimal in ().

The same result for the signature [4,3] would obviously be

01 : 0.7 (1)
10 : 0.3 (2)

3rd input - quantum circuit

You enter a list of quantum gates here in the following format [gate1, gate2, ..., gaten]. You can also add measurements to this list, they are represented by M(.).

Run Button

OK, after you've entered the initial state (if you don't, the default state is 0) and quantum circuit, you press the Run button, which applies the quantum circuit to the qregister and displays the end state and probabilities after a hypothetical measurement of the qubits listed in qubit signature (2nd input). For example:

01 : 0.5 (1)
10 : 0.5 (2)

(0.707106781187,0)|1>
(0.707106781187,0)|2>

The first list shows the probabilities described in 2nd input - qubit signature section. The second list is just a state of the qregister (a complex vector).

Load Button

When you create some more complex and long circuit, you want to have it in a saved text file. You can. Write your circuit in a text file using your favorite editor, save it on your drive and then just press Load to load it into the Quantum Simulator.

Doesn't work under IE, so please use some other browser for this feature.

Specification

Supported gates

H(bit) [Hadamard Gate]

Defined on base vectors $|[bit]\rangle$ :

$H|0\rangle = \frac{1}{\sqrt{2}}(|0\rangle + |1\rangle)$

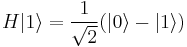
$H|1\rangle = \frac{1}{\sqrt{2}}(|0\rangle - |1\rangle)$

X(bit) [Pauli X-gate]

Defined on base vectors $|[bit]\rangle$ :

$X|0\rangle = |1\rangle$

$X|1\rangle = |0\rangle$

Y(bit) [Pauli Y-gate]

Defined on base vectors $|[bit]\rangle$ :

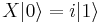
$X|0\rangle = i|1\rangle$

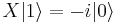
$X|1\rangle = -i|0\rangle$

Z(bit) [Pauli Z-gate]

Defined on base vectors $|[bit]\rangle$ :

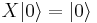
$X|0\rangle = |0\rangle$

$X|1\rangle = -|1\rangle$

R(n, bit) [Phase Shift Gate]

Defined on base vectors $|[bit]\rangle$ :

$R_n|0\rangle = |0\rangle$

$R_n|1\rangle = e^{i\pi/2^n}|1\rangle$

CNot(control, bit) [Controled Not Gate]

Defined on base vectors $|[control][bit]\rangle$ :

$CNot|00\rangle = |00\rangle$

$CNot|01\rangle = |01\rangle$

$CNot|10\rangle = |11\rangle$

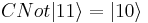
$CNot|11\rangle = |10\rangle$

CCNot(control1, control2, bit) [Toffoli Gate]

Defined on base vectors $|[control1][control2][bit]\rangle$ :

$CCNot(|c_1c_2b>) = |c_1c_2(c_1\cdot c_2\oplus b)\rangle$

C(control, gate) [Universal Control Gate]

Defined on base vectors $|[control]x\rangle$ :

$C(gate)(|0\rangle|x\rangle) = |0\rangle|x\rangle$

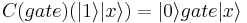
$C(gate)(|1\rangle|x\rangle) = |0\rangle gate|x\rangle$

U([argbit₀, ...,argbit_n],[valbit₀, ...,valbit_m], function) [Universal Function Gate]

Defined on base vectors $|[argbit_n]\dots[argbit_0]\rangle|[valbit_m]\dots[valbit_0]\rangle$ :

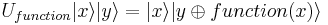
$U_{function}|x\rangle|y\rangle = |x\rangle|y \oplus function(x)\rangle$

Hidden Console

jQ has an additional advanced feature — Hidden Console. When you place the cursor in the last file of the black window in the left you can enter some special directives. Bellow you will find a full list of Hidden Console directives:

clr()

Clears window.

load()

The same as button Load.

measure(bit)

Performs a measurement on a chosen bit. To see the result, you need to type prob([[bit]]). Changes the qregister state.

prob([signature₁, signature₂, ..., signature_n])

Displays the states of chosen qubits with probabilities after a series of hypothetical measurements. Doesn't change the qregister state. The value of state is binary grouped. Each group is defined by corresponding signature. Consider following example. Assume that the qregister state is:

(0.5,0)|0>
(0.5,0)|1>
(0.5,0)|4>
(0.5,0)|5>

The corresponding probabilities are:

000 : 0.25 (0)
001 : 0.25 (1)
100 : 0.25 (4)
101 : 0.25 (5)

After typing in Hidden Console prob( [ [0], [1,2] ] )

You will see the same result in different representation:

|0>|0>:0.25
|0>|1>:0.25
|2>|0>:0.25
|2>|1>:0.25

For prob( [ [0,1], [2] ]):

|0>|0>:0.25
|0>|1>:0.25
|1>|0>:0.25
|1>|1>:0.25

reset(n)

Set the initial state of qregister to n.

run()

The same as the Run button.

state()

Displays current state (complex vector) of qregister.

@@ Line 10: / Line 10: @@
 === 1st input - init state ===
 [[File:1st.png]]
-You enter init state of qubits here. A decimal integer is required here. Its binary representation defines the start states of the qubits in qregister. '''Qubit 0 is at the top'''.
+You enter the init state of qubits here. A decimal integer is required here. Its binary representation defines the start states of the qubits in qregister. '''Qubit 0 is at the top'''.
 === 2nd input - qubit signature ===

Difference between revisions of "JQ Manual"

Revision as of 16:24, 22 May 2013

Contents

Quick Overview

1st input - init state

2nd input - qubit signature

3rd input - quantum circuit

Run Button

Load Button

Specification

Supported gates

H(bit) [Hadamard Gate]

X(bit) [Pauli X-gate]

Y(bit) [Pauli Y-gate]

Z(bit) [Pauli Z-gate]

R(n, bit) [Phase Shift Gate]

CNot(control, bit) [Controled Not Gate]

CCNot(control1, control2, bit) [Toffoli Gate]

C(control, gate) [Universal Control Gate]

U([argbit₀, ...,argbit_n],[valbit₀, ...,valbit_m], function) [Universal Function Gate]

Hidden Console

clr()

load()

measure(bit)

prob([signature₁, signature₂, ..., signature_n])

reset(n)

run()

state()

Personal tools

Namespaces

Variants

Views

Actions

Search

Navigation

Toolbox

Difference between revisions of "JQ Manual"

Revision as of 16:24, 22 May 2013

Contents

Quick Overview

1st input - init state

2nd input - qubit signature

3rd input - quantum circuit

Run Button

Load Button

Specification

Supported gates

H(bit) [Hadamard Gate]

X(bit) [Pauli X-gate]

Y(bit) [Pauli Y-gate]

Z(bit) [Pauli Z-gate]

R(n, bit) [Phase Shift Gate]

CNot(control, bit) [Controled Not Gate]

CCNot(control1, control2, bit) [Toffoli Gate]

C(control, gate) [Universal Control Gate]

U([argbit0, ...,argbitn],[valbit0, ...,valbitm], function) [Universal Function Gate]

Hidden Console

clr()

load()

measure(bit)

prob([signature1, signature2, ..., signaturen])

reset(n)

run()

state()

Personal tools

Namespaces

Variants

Views

Actions

Search

Navigation

Toolbox

U([argbit₀, ...,argbit_n],[valbit₀, ...,valbit_m], function) [Universal Function Gate]

prob([signature₁, signature₂, ..., signature_n])